Infinite Bases for EQ kernel

I understand that the EQ kernel (and other kernels) can be understood via the kernel trick as an infinite number of (appropriate) bases functions. I’ve not found the actual proof of this online (I’m sure it’s somewhere, but I clearly didn’t know what to search for [edit: Turns out some of it is in the covariance functions chapter in Gaussian Processes for Machine Learning]). It’s straightforward, but I wanted to see it, so I would know what constants etc I needed my bases to have (lengthscale and height).

Without loss of generality (hopefully) I’ve just considered the kernel evaluated between $x$ and $0$ . This should be fine as the EQ kernel is stationary.

So:

The EQ kernel: $k(x,0) = e^{-\frac{x^2}{2l^2}}$

We believe that an infinite number of Gaussian bases, $\phi_a(x) = \left(\frac{l^2 \pi}{2}\right)^{-\frac{1}{4}}e^{-\frac{(x-a)^2}{l^2}}$ will produce the EQ kernel.

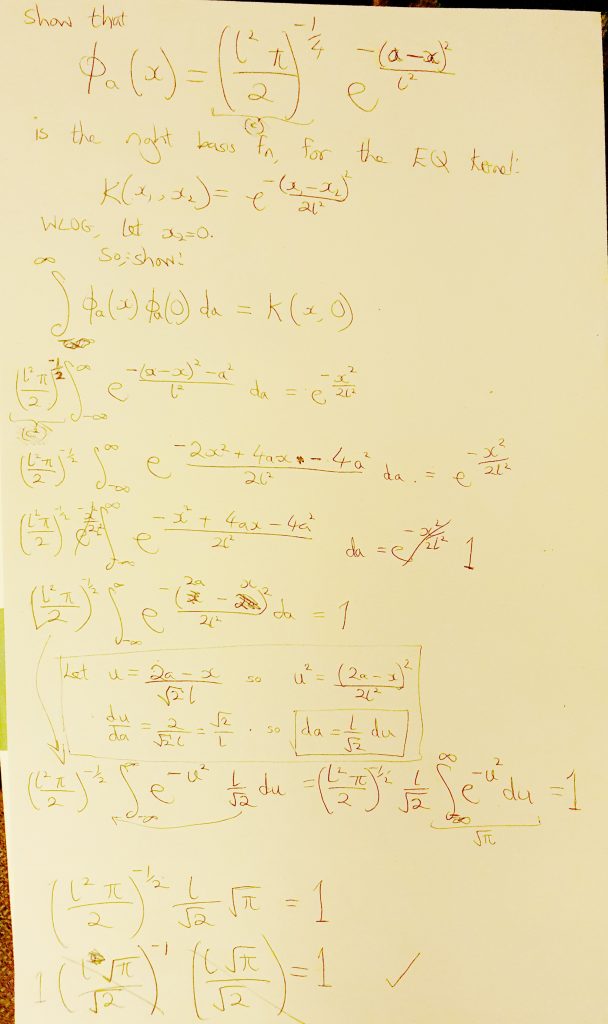
mathematical derivation/proof (will copy into latex sometime).

For multiple dimensional inputs:

The EQ kernel: $k(\mathbf{x},0) = e^{-\sum_i(\frac{x_i}{l_i})^2}$

We believe that an infinite number of Gaussian bases, $\phi_\mathbf{a}(\mathbf{x}) = \prod{l_i}^{-\frac{1}{2}}\left(\frac{\pi}{2}\right)^{-\frac{D}{4}}e^{-\sum_i (\frac{(x_i-a_i)}{l_i})^2}$ will produce the EQ kernel.