In the last post, we looked at methods to find the optimum landmark. In this post we look at how to find one’s location given a set of landmarks.
Previously I’ve naively found the probability of each location on a grid, given the reported distances to the landmarks, then sampled from this grid to find the probability for each output area.
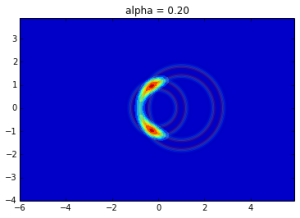
In this notebook we approach the problem differently, and look for the probability of the set of distances to the landmarks given the output area. By swapping the order, we are able to use the node in the Bayesian network.